大電網(wǎng)靜態(tài)穩(wěn)定態(tài)勢評估的大數(shù)據(jù)融合方法
近年來,新一代智能電網(wǎng)調(diào)度技術(shù)支持系統(tǒng)實現(xiàn)了電網(wǎng)靜態(tài)和動態(tài)信息的采集功能,隨著廣域測量系統(tǒng)(wide area measurement system,WAMS)在工程中廣泛應用,WAMS系統(tǒng)可在時空統(tǒng)一角度且具有足夠的精度和速度測量電網(wǎng)真實運行狀態(tài)信息,為大電網(wǎng)穩(wěn)定態(tài)勢評估帶來新的契機。
靜態(tài)穩(wěn)定態(tài)勢分析通常采用模型仿真,但是每次仿真分析前需要確定全部數(shù)學模型,參數(shù)及仿真場景,故計算量大,存在維數(shù)災難,且難以計及非常規(guī)數(shù)據(jù)的影響,仍需要花費大量時間和精力。模型法分析結(jié)果的準確性取決于機理模型的準確性,建模過程中的各種簡化和假設使模型法的分析結(jié)果不能充分反映電網(wǎng)實際運行狀況。此外,隨著電網(wǎng)規(guī)模擴大、電網(wǎng)有些區(qū)域會接近輸電極限,加之大規(guī)模間歇性新能源(renewable energy systems,RES)并網(wǎng)發(fā)電大大增加了電力生產(chǎn)的不確定性和電網(wǎng)運行困難;大規(guī)模電動汽車(electric vehicle,EV)充放電又增加了電力負荷的隨機性,這些各個環(huán)節(jié)不確定因素及其交互影響使得電網(wǎng)穩(wěn)定行為更為復雜,傳統(tǒng)研究假設條件可能會不成立。
大數(shù)據(jù)技術(shù)近年來受到廣泛關(guān)注,它對大量多源數(shù)據(jù)進行高速捕捉、發(fā)現(xiàn)和分析,利用經(jīng)濟的方法提取有價值的技術(shù)體系或架構(gòu)。廣義上講,大數(shù)據(jù)不僅指所涉及的數(shù)據(jù),還包含了對這些數(shù)據(jù)進行處理和分析的理論、方法和技術(shù)。隨著我國智能電網(wǎng)建設的不斷推進和深入,電網(wǎng)量測體系積累了大量的數(shù)據(jù),這就使得大數(shù)據(jù)分析挖掘技術(shù)在靜態(tài)穩(wěn)定態(tài)勢評估具有可行性。
目前,電網(wǎng)存在各種類型的大量仿真或?qū)崪y數(shù)據(jù),啟發(fā)人們思考如何用數(shù)據(jù)分析取代機理建模,從而提出了數(shù)據(jù)驅(qū)動模式。然而,幾乎所有關(guān)于大數(shù)據(jù)的論文都會強調(diào)不同類型數(shù)據(jù)之間的融合,但卻鮮有討論如何融合。
針對以上問題,本文提出了基于隨機矩陣理論的靜態(tài)穩(wěn)定態(tài)勢評估方法。隨機矩陣理論作為一種普適性的大數(shù)據(jù)分析方法,無需詳細物理模型,可綜合考慮歷史數(shù)據(jù)和實時數(shù)據(jù),具有從高維角度認識復雜系統(tǒng)等優(yōu)點。隨機矩陣是對復雜網(wǎng)絡進行統(tǒng)計分析的重要數(shù)據(jù)理論之一,通過對復雜系統(tǒng)的能譜和本征態(tài)進行統(tǒng)計分析,揭示數(shù)據(jù)中整體的行為特征,可以從宏觀上對復雜系統(tǒng)的性質(zhì)進行研究分析。隨機理論是近年來的研究熱點之一,在量子物理、金融工程、醫(yī)療等多個領(lǐng)域發(fā)揮了重要作用。文獻[8]首次將隨機矩陣理論引入電力系統(tǒng),提出一種全新的、通用的大數(shù)據(jù)分析架構(gòu),將其應用于電力系統(tǒng)異常發(fā)現(xiàn);文獻提出一種基于隨機矩陣理論的配電網(wǎng)運行狀態(tài)相關(guān)性分析方法;文獻提出基于高維隨機矩陣描述的WAMS量測大數(shù)據(jù)建模與分析方法;文獻提出一種基于高維隨機矩陣大數(shù)據(jù)分析模型的輸變電設備關(guān)鍵性能評估方法;文獻提出一種隨機矩陣在全球能源互聯(lián)網(wǎng)中的應用框架。然而,大數(shù)據(jù)技術(shù)在電力系統(tǒng)中的應用鮮有涉及如何對靜態(tài)穩(wěn)定態(tài)勢進行評估的介紹。高維隨機矩陣理論作為新興的大數(shù)據(jù)分析方法,能將各類數(shù)據(jù)集成到高維矩陣中,從概率和統(tǒng)計角度研究矩陣的特性和數(shù)據(jù)分布情況。
本文提出了一種電網(wǎng)靜態(tài)穩(wěn)定態(tài)勢評估的大數(shù)據(jù)融合方法,利用歷史數(shù)據(jù)和實時數(shù)據(jù)建立了隨機矩陣模型。在此基礎(chǔ)上,提出了兩種基于隨機矩陣理論的極限譜分布函數(shù),用來研究矩陣特性和數(shù)據(jù)分布情況。進而,利用平均譜半徑實現(xiàn)靜態(tài)穩(wěn)定態(tài)勢評估。最后,利用IEEE39節(jié)點系統(tǒng)算例仿真,驗證了所提方法的有效性。
1大數(shù)據(jù)融合方法
1.1基于隨機矩陣理論的大數(shù)據(jù)融合方法
電力系統(tǒng)實際運行中,發(fā)生穩(wěn)定破壞性故障相對罕見,導致實測數(shù)據(jù)缺乏失穩(wěn)數(shù)據(jù),難以進行數(shù)據(jù)挖掘,通常采用仿真計算來獲得樣本。連續(xù)潮流法是電網(wǎng)靜態(tài)(電壓)穩(wěn)定分析的有效工具,可用于模擬實際電網(wǎng)中發(fā)電負荷區(qū)域性增長的遠景和規(guī)劃[17-18]。本文進行分析挖掘的數(shù)據(jù)采用基于負荷增長的連續(xù)潮流法(ContinuationPowerFlow,CPF)進行仿真得到大量的樣本數(shù)據(jù);由于在數(shù)據(jù)采集和傳輸過程中會產(chǎn)生隨機噪聲,電力系統(tǒng)存在小幅度隨機擾動。因此,本文在連續(xù)潮流仿真數(shù)據(jù)基礎(chǔ)上添加高斯白噪聲,以此數(shù)據(jù)來模擬電網(wǎng)實際運行獲得的數(shù)據(jù)。
隨機矩陣理論中漸進收斂性要求矩陣的維數(shù)趨近無窮,在處理實際工程問題時,當維數(shù)從幾十到幾百時,也能觀察到相當精確的漸進收斂結(jié)果[15]。在矩陣構(gòu)造時,對行列元素通過調(diào)整來獲得最優(yōu)的行列比值。
對于電力網(wǎng)絡,選擇nn個節(jié)點的量測數(shù)據(jù)作為空間樣本,每個節(jié)點有kk個狀態(tài)變量,構(gòu)成NN個變量,其中N=n×k。
在采樣時刻titi,每個節(jié)點的量測數(shù)據(jù)可以構(gòu)成一個列向量:
x(ti)=[x1,x2,?,xN]Tx(ti)=[x1,x2,?,xN]T(1)
將每個節(jié)點采樣時刻的量測數(shù)據(jù)按照時間序列排序,可形成如下矩陣:
XN×T=[x(t1),x(t2),?,x(ti),?]∈CN×TXN×T=[x(t1),x(t2),?,x(ti),?]∈CN×T(2)
該矩陣即為大數(shù)據(jù)分析的數(shù)據(jù)源,這些數(shù)據(jù)按照時間順序采樣,不同節(jié)點的電氣特征量具有空間特性,將兩者結(jié)合起來則構(gòu)成具有時空特性的數(shù)據(jù)源。
1.2靜態(tài)穩(wěn)定態(tài)勢評估的輸入數(shù)據(jù)
電網(wǎng)的運行狀態(tài)由多種狀態(tài)變量表征,比如電網(wǎng)各個節(jié)點的電壓和相角、發(fā)電機注入有功功率和無功功率、負荷有功功率和無功功率、支路電流等。電網(wǎng)中各元件間的拓撲關(guān)系及相互作用力必然蘊含于廣域時空量測信息中。此外,電網(wǎng)的運行狀態(tài)還受到各種電氣因素和非電氣因素的影響。電氣因素包括分布式電源出力、各類故障和擾動等;非電氣因素包括溫度、濕度、風速等氣候因素和社會經(jīng)濟因素等。在大數(shù)據(jù)分析時,根據(jù)具體的研究目的和數(shù)據(jù)資源選取量測數(shù)據(jù)進行數(shù)據(jù)源隨機矩陣的構(gòu)建。
在采樣時,由于不同數(shù)據(jù)的采樣頻率可能不同,可以認為采樣頻率低的數(shù)據(jù)類型在采樣間隔內(nèi)數(shù)值相等。在矩陣分析時,要將所有元素進行標準化處理,其目的是去量綱化和數(shù)值歸一化,從而使得各個指標具有可比性。
在研究靜態(tài)電壓穩(wěn)定性時,由于電壓失穩(wěn)是負荷驅(qū)動的,側(cè)重研究負荷和電壓數(shù)據(jù),電壓穩(wěn)定性問題就是負荷的穩(wěn)定性問題。故而本文在研究靜態(tài)穩(wěn)定態(tài)勢評估時,選取每個節(jié)點的節(jié)點電壓數(shù)據(jù)和所有負荷節(jié)點的有功功率數(shù)據(jù)構(gòu)造矩陣。為了實現(xiàn)數(shù)據(jù)的實時分析,采用文獻[13]中提出的實時分離窗技術(shù),該技術(shù)可以從數(shù)據(jù)源中獲取當前時刻和歷史時刻的采樣量測數(shù)據(jù),實時分離窗的寬度為Tw,在采樣時刻ti,獲得的數(shù)據(jù)矩陣為:
XN×Tw(ti)=[x(ti−Tw+1),x(ti−Tw+2),?,x(ti)]XN×Tw(ti)=[x(ti−Tw+1),x(ti−Tw+2),?,x(ti)](3)
該技術(shù)也可以對噪聲數(shù)據(jù)進行平滑處理。
2隨機矩陣理論基本原理
2.1隨機矩陣理論
隨機矩陣理論有兩個基本概念,經(jīng)驗譜分布函數(shù)和極限譜分布函數(shù)。對于任意特征值為實數(shù)的n×nn×n維隨機矩陣A,稱函數(shù)
FA(x)=1n∑i=1nI(λAi≤x)FA(x)=1n∑i=1nI(λiA≤x)(4)
為矩陣A的經(jīng)驗譜分布函數(shù)(empiricalspectrumdistribution,ESD),這里λAiλiA為矩陣A的特征根,i=1,?,ni=1,?,n,I(•)表示指示性函數(shù)。我們把經(jīng)驗譜分布函數(shù)的極限稱為極限譜分布函數(shù)。經(jīng)驗譜分布函數(shù)是隨機的,但通常極限譜分布函數(shù)是非隨機的,如圓率,半圓率、M-P率(Marchenko-PaturLaw)和圓環(huán)率。
對于高維數(shù)據(jù)源X矩陣,其樣本協(xié)方差陣如下式所示:
Sn=1n(∑i=1nxix′i)=1nXX′Sn=1n(∑i=1nxix′i)=1nXX′(5)
可求得其經(jīng)驗譜分布函數(shù)FSn(x)FSn(x),通過對其進行Stieltjes變換[19-21],利用Stieltjes變換法,可以把對隨機矩陣經(jīng)驗譜分布函數(shù)研究轉(zhuǎn)換為對隨機矩陣逆的跡的研究,由此求得極限譜分布函數(shù)。
2.2M-P率和圓環(huán)率
利用隨機矩陣理論評估靜態(tài)穩(wěn)定態(tài)勢重點,是根據(jù)極限譜分布函數(shù)的變化規(guī)律來評估靜態(tài)穩(wěn)定裕度。下文將介紹兩種極限譜分布函數(shù)M-P率和圓環(huán)率[12,22-23]。
采用M-P率觀測譜分布,M-P率其極限譜密度如式(6)。
式中,a=σ2(1−c√)2a=σ2(1−c)2,b=σ2(1+c√)2b=σ2(1+c)2這里c為維數(shù)與樣本量的比值,σ2σ2為刻度參數(shù),σ2=1σ2=1。通過對連續(xù)潮流輸入數(shù)據(jù)預處理后,應用實時分離窗技術(shù),選取不同狀態(tài)可以看出樣本協(xié)方差譜分布直方圖和M-P率曲線如圖1所示。
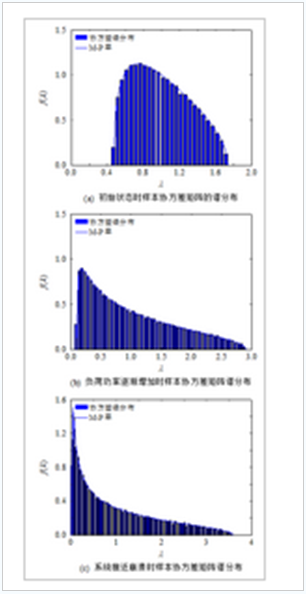
圖1樣本協(xié)方差矩陣譜分布
圖中展示了隨著負荷的不斷增長,樣本協(xié)方差矩陣譜分布直方圖變窄變長。可以明顯看出電力系統(tǒng)發(fā)生了變化。
由于輸入數(shù)據(jù)的高維矩陣X中所含元素均為實數(shù),通過利用酉矩陣U對X的樣本協(xié)方差矩陣進行處理后可將特征值映射到復平面。樣本協(xié)方差矩陣X經(jīng)過奇異化處理后得到等效矩陣Xu=UXX′−−−−√Xu=UXX′[24-25],U為haar矩陣,滿足XuXTu=XXTXuXuT=XXT。對該矩
- 相關(guān)閱讀
- 熱門技術(shù)
- 電力通信
- 智能電網(wǎng)
- 云計算
- 大數(shù)據(jù)
-
2017年云計算市場營收增長24%,達1800億美元
2018-01-10市場 -
人人稱道的云計算,市場發(fā)展仍存幾大障礙
-
當春運遇上云計算
2018-01-10當春運遇上云計算
-
國家標準《智能電網(wǎng)調(diào)度控制系統(tǒng)技術(shù)規(guī)范第二部分:術(shù)語》已發(fā)布并實施
-
盤點|2017年實施的電力相關(guān)行業(yè)標準(DL、NB)
-
大電網(wǎng)靜態(tài)穩(wěn)定態(tài)勢評估的大數(shù)據(jù)融合方法
-
2017年云計算市場營收增長24%,達1800億美元
2018-01-10市場 -
人人稱道的云計算,市場發(fā)展仍存幾大障礙
-
當春運遇上云計算
2018-01-10當春運遇上云計算